Important Dimensionless Numbers & Their Significance
Nomenclature:
D = diameter of pipe
DH = Hydraulic diameter
L = Length of the pipe
Lch = characteristic length
R = Length through which conduction occurs.
u = mean characteristic velocity of the object relative to the fluid.
Vch = Characteristic velocity
Cp = specific heat capacity at constant pressure.
k = thermal conductivity
μ = dynamic viscosity of the fluid
 = density of fluid.
= density of fluid.
DAB = mass diffusivity
h = heat transfer coefficient.
g = acceleration due to earths gravity.
t = characteristic time
ν = Kinematic viscosity of fluid.
α = Thermal diffusivity
β = volumetric thermal expansion coefficient ( = 1/T for ideal fluids, T = absolute temperature)
Ts = surface temperature
T∞ = Bulk Temperature
Reynolds Number :
The dimensionless Reynolds number plays a prominent role in foreseeing the patterns in a fluid’s behavior. The Reynolds number, referred to as Re, is used to determine whether the fluid flow is laminar or turbulent. It is one of the main controlling parameters in all viscous flows where a numerical model is selected according to pre-calculated Reynolds number.
Significance:
- Ratio of Inertial forces to viscous forces.
- Primarily used to analyse different flow regimes namely Laminar, Turbulent, or both.
- When Viscous forces are dominant its a laminar flow & when Inertial forces are dominant it is a Turbulent flow.
=======X=======X=======X=======X=======X======X=======X=======X====



Prandtl Number :
Prandtl number is defined as the ratio of Kinematic viscosity ( ν ) and thermal diffusibility (α). Kinematic viscosity can also be called momentum diffusibility ; it shows the relative thickness of the velocity boundary layer to the thermal boundary layer.
Pr−no=ν/α
for example:- if Pr>1, that means momentum diffusivity > heat diffusivity, which means for the same distance travelled along the flow,velocity layer will be thicker than the thermal boundary layer or in other sense, less distance to be travelled along the flow for the same thickness of the velocity boundary layer to fully develop as compared to the distance travelled along the flow for the same thickness of thermal boundary layer for the same.
Also velocity boundary layer is thicker than the thermal boundary layer which further means that the given fluid has the ability to transport the momentum faster through the fluid as compared to the heat transfer by the conduction, which in a way means convection dominates over the conduction.
Significance:
- Depends only on fluid & its properties. It is also ratio of velocity boundary layer to thermal boundary layer
- Pr = small, implies that rate of thermal diffusion (heat) is more than the rate of momentum diffusion (velocity).
- Also the thickness of thermal boundary layer is much larger than the velocity boundary layer.
=======X=======X=======X=======X=======X======X=======X=======X====
Schmidt number
The Schmidt number (Sc) is the ratio of the kinematic viscosity to the molecular diffusion coefficient.
Schmidt number is the mass transfer equivalent of Prandtl Number. For gases, Sc and Pr have similar values (≈ 0.7) and this is used as the basis for simple heat and mass transfer analogies
Significance:
- Analogous of Prandtl number in Heat Transfer.
- Used in fluid flows in which there is simultaneous momentum & mass diffusion.
- It is also ratio of fluid boundary layer to mass transfer boundary layer thickness.
- To find mass transfer coefficient using Sherwood number, we need Schmidt number.
=======X=======X=======X=======X=======X======X=======X=======X====
Lewis number is a dimensionless number which is the ratio of thermal Diffusivity to mass Diffusivity (or) Schmidt number to Prandtl number. This is used to characterize flows in which there is simultaneous heat and mass (by convection) transfer. If Lewis number is greater than one item explains the predominance of concentration boundary layer. If it’s equal to one it either gives the transfer of both mass and heat or the presence of velocity boundary layer which hinders the transport of heat and mass.
Significance:
- Ratio of thermal diffusivity to mass diffusivity.
- Fluid flow with simultaneous Heat & mass transfer by convection.
- It is also ratio of Schmidt number to Prandtl number
=======X=======X=======X=======X=======X======X=======X=======X====

Peclet Number :
The Peclet number is a dimensionless number used in calculations involving convective heat transfer. It is the ratio of the thermal energy convected to the fluid to the thermal energy conducted within the fluid. If Pe is small, conduction is important and in such a case, the major source of conduction could be down the walls of a tube. The Peclet number is the product of the Reynolds number and the Prandtl number. It depends on the heat capacity, density, velocity, characteristic length and heat transfer coefficient.
Significance:
- Heat transported by convection to Heat transported by conduction.
- Product of Re & Pr for Pe(HT) & product of Re & SC for Pe(MT)
=======X=======X=======X=======X=======X======X=======X=======X====
Stanton Number :
The Stanton number, St, is a dimensionless number that measures the ratio of heat transferred into a fluid to the thermal capacity of fluid. The Stanton number is named after Thomas Edward Stanton (1865–1931).[1] It is used to characterize heat transfer in forced convection flows.

where
- h = convection heat transfer coefficient
- ρ = density of the fluid
- cp = specific heat of the fluid
- u = speed of the fluid
It can also be represented in terms of the fluid’s Nusselt, Reynolds, and Prandtl numbers:

where
- Nu is the Nusselt number;
- Re is the Reynolds number;
- Pr is the Prandtl number
Significance:
- It is the ratio of heat transferred to the fluid to the heat transported by the fluid (ratio of Nusselt number to Peclet number)
- Used to findheat transfer in forced convection flows.
- St(HT) = Nu/(Re.Pr) & St(MT) = Sh/(Re.Sc)
=======X=======X=======X=======X=======X======X=======X=======X====
Significance:
A) Sherwood Number:
- Ratio ofConvective to diffusive mass transport.Used in mass transfer operations.
- Analogous of Nusselt number in Heat transfer OR Sherwood number is Nusselt number for mass transfer.
B) Nusselt Number
- Ratio of convective to conductive heat transfer coefficient across the boundary layer.
- Low Nu => conduction is more => Laminar flow
- High Nu => convection is more=> Turbulent flow.
- It can also be viewed as conduction resistance to convection resistance of the material.
- Free convection: Nu = f(Ra, Pr)
- Forced Convection: Nu = f(Re, Pr)
=======X=======X=======X=======X=======X======X=======X=======X====
Significance:
- Ratio of Buoyancy force to viscous force in natural convection.
- Reynolds number is used in forced convection of fluid flow, whereas Grashof number is used in natural convection.
=======X=======X=======X=======X=======X======X=======X=======X====
Significance:
- used in unsteady state (transient) heat transfer conditions.
- ratio of heat transfer resistance inside the body to heat transfer resistance at the surface of the body. OR ratio of internal thermal resistance to external thermal resistance .
- Shows the variation of temperature inside the body w.r.t to time.
- Bi < 0.1 => heat transfer resistance inside the body is very low => inside the body conduction takes place faster compared to convection at the surface. => no temperature gradient inside the body (uniformity in temperature) vice versa implies that Temperature is not uniform throughout hte material volume.
=======X=======X=======X=======X=======X======X=======X=======X====
Significance:
- It shows the presence & strength of convection in a fluid body.
- Heat transfer by Conduction within fluid < Critical value for that fluid < Heat transfer by convection. (consequences of Ra values)
- Product of Gr.Pr
=======X=======X=======X=======X=======X======X=======X=======X====
- Characterizes laminar flow in a conduit OR transfer of heat by streamline fluid flow in a pipe
- In case of mass transfer, Pr is replaced by Sc.
=======X=======X=======X=======X=======X======X=======X=======X====
Significance:
- Ratio of rate of heat conduction to the rate of heat storage.
- Used along with Biot number to solve transient state heat transfer problems.
- For mass transfer by diffusion, Fourier number for MT is used.
- It can also be understood as current time to the time taken to reach steady state.
|
|
| = |
specific heat |
| latent heat |
|
Note: Stefan number is useful in the study of heat transfer during phase change.
|
|
| = |
stopping distance of a particle |
| characteristic dimension of the obstacle |
|
Note: Commonly used in particles suspended in fluid.
For Stk << 1, the particle negotiates the obstacle.
For Stk >> 1, the particle travels in straightline and eventually collides with obstacle.
- Strouhal Number (for oscillatory flow):
|
|
| = |
inertia (local) |
| inertia (convection) |
|
Note: If tref is taken as the reciprocal of the circular frequency ω of the system, then
where L = [ri(ro − ri)3]1/4
|
|
| = |
inertial force |
| surface tension force |
|
=======X=======X=======X=======X=======X======X=======X=======X====
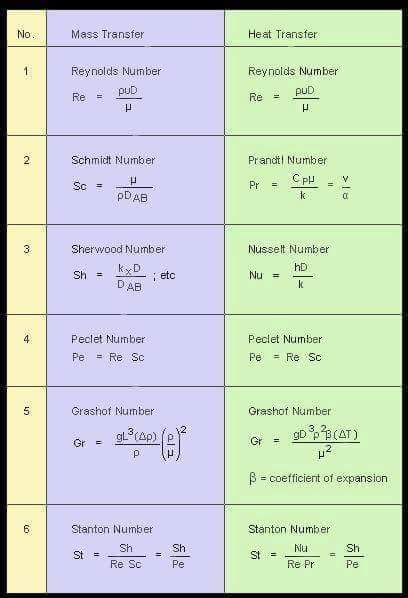
Summary of Important Dimensionless Number in A Glance

ImageSource : Heat Transfer ; SlideShare
ArticleSource : Chemical Files
Also Read Another Content:
 = density of fluid.
= density of fluid.
































google porn porn google